Intel Distribution For Python To Create A Genetic Algorithm

Python Genetic Algorithm

Genetic algorithms (GA) simulate natural selection to solve finite and unconstrained optimization problems. Traditional methods take time and resources to address NP-hard optimization problems, but these algorithms can do it. GAs are based on a comparison between human chromosomal behavior and biological evolution.

This article provides a code example of how to use numba-dpex for Intel Distribution for Python to create a generic GA and offload a calculation to a GPU.

Genetic Algorithms (GA)

Activities inside GAs

Selection, crossover, and mutation are three crucial biology-inspired procedures that may be used to provide a high-quality output for GAs. It’s critical to specify the chromosomal representation and the GA procedures before applying GAs to a particular issue.

Selection

This is the procedure for choosing a partner and recombining them to produce children. Because excellent parents encourage their children to find better and more appropriate answers, parent selection is critical to the convergence rate of GA.

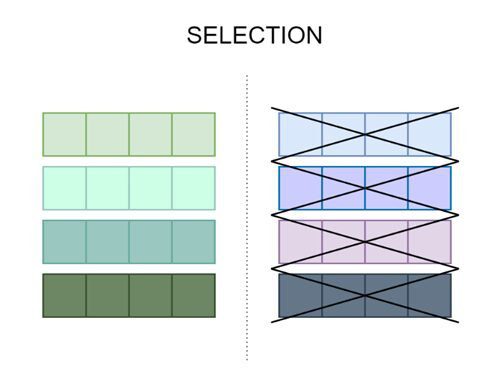
Figure 1 shows an illustration of the selection procedure whereby the following generation’s chromosomes are reduced by half.

The extra algorithms that decide which chromosomes will become parents are often required for the selection procedure.

Crossover

Biological crossover is the same procedure as this one. In this case, more than one parent is chosen, and the genetic material of the parents is used to make one or more children.

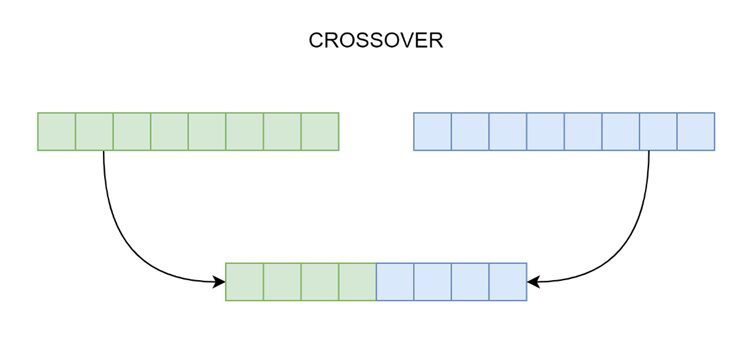
Figure 2: A crossover operation in action.

As shown in figure 2, the crossover procedure produces kid genomes from specific parent chromosomes. There is only one kid genome produced and it may be a one-point crossing. The first and second parents each give the kid half of their DNA.

Mutation

A novel answer may be obtained by a little, haphazard modification to the chromosome. It is often administered with little probability and is used to preserve and add variation to the genetic population.

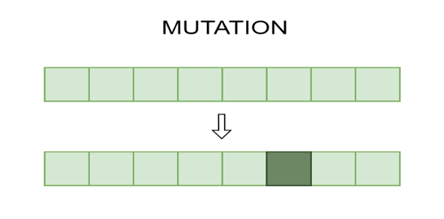
Figure 3: A mutation procedure involving a single chromosomal value change.

As shown in figure 3, the mutation procedure may alter a chromosome.

Enhance Genetic Algorithms for Python Using Intel Distribution

With libraries like Intel oneAPI Data Analytics Library (oneDAL) and Intel oneAPI Math Kernel Library (oneMKL), developers may use Intel Distribution for Python to obtain near-native code performance. With improved NumPy, SciPy, and Numba, researchers and developers can expand compute-intensive Python applications from laptops to powerful servers.

Use the Data Parallel Extension for Numba (numba-dpex) range kernel to optimize the genetic algorithm using the Intel Distribution for Python. Each work item in this kernel represents a logical thread of execution, and it represents the most basic kind of data-parallel and parallelism across a group of work items.

Let’s see an example of how the kernel for a vector-add operation is implemented:

import dpnp
import numba_dpex

@numba_dpex.kernel
def vector_add(item: numba_dpex.kernel_api.Item, a, b, c):
    i = item.get_id(0)
    c[i] = a[i] + b[i]

Create the three vectors, a, b, and c, to execute this code. Data goes into a and b, and the outcome of the operation is stored in c. After that, the vectors must be sent to a particular device such as a GPU and the kernel must be executed as follows:

N = 1024
a = dpnp.ones(N, device="gpu")
b = dpnp.ones_like(a, device="gpu")
c = dpnp.zeros_like(a, device="gpu")
 
numba_dpex.call_kernel(vector_add, numba_dpex.kernel_api.Range(N), a, b, c)

The vector-add operation was carried out on a GPU in the prior code, and vector c held the result. In a similar vein, the implementation is the same for every other function or method.

Code Execution

Refer to the code sample for instructions on how to develop the generic GA and optimize the method to operate on GPUs using numba-dpex for Intel Distribution for Python. It also describes how to use the various GA operations selection, crossover, and mutation and how to modify these techniques for use in solving other optimization issues.

Set the following values to initialize the population:

• 5,000 people live there.
• Size of a chromosome: 10
• Generations: 5.

There are ten random floats between 0 and 1 on each chromosome.

• Put the GA into practice by developing an assessment strategy: This function serves as numba-dpex’s benchmark and point of comparison. The calculation of an individual’s fitness involves using any combination of algebraic operations on the chromosome.
• Carry out the crossover operation: The inputs are first and second parents to two distinct chromosomes. One more chromosome is returned as the function’s output.
• Carry out the mutation operation: There is a one percent probability that every float in the chromosome will be replaced by a random value in this code example.
• Put into practice the selection process, which is the foundation for producing a new generation. After crossover and mutation procedures, a new population is generated inside this function.
• Launch the prepared functions on a CPU, beginning with a baseline. Every generation includes the following processes to establish the first population:
• Utilizing the eval_genomes_plain function, the current population is evaluated
• Utilizing a next_generation function, create the next generation.
• Wipe fitness standards, since a new generation has already been produced.
• Measured and printed is the calculation time for those operations. To demonstrate that the calculations were the same on the CPU and GPU, the first chromosome is also displayed.
• Run on a GPU: Create an evaluation function for the GPU after beginning with a fresh population initialization (similar to step 2). With GPU implementation, chromosomes are represented by a flattened data structure, which is the sole difference between it and CPU implementation. Also, utilize a global index and kernels from numba-dpex to avoid looping over every chromosome.
• The time for assessment, generation production, and fitness wipe is monitored when a GPU is operating, just like it is for the CPU. Deliver the fitness container and all of the chromosomes to the selected device. After that, a kernel with a specified range may be used.

Conclusion

Use the same procedures for further optimization issues. Describe the procedures of chromosomal selection, crossing, mutation, and assessment. The algorithm is executed the same way in its entirety.

Execute the above code sample and evaluate how well this method performs while executing sequentially on a CPU and parallelly on a GPU. The code result shows that using a GPU-based numba-dpex parallel implementation improves performance speed.