What is Quantum Algorithms and How it works

A quantum algorithms is a process designed for quantum computers that control the principles of quantum mechanics, like superposition, entanglement, and interference, to perform tasks more proficiently than classical algorithms.

 Characteristics of Quantum Algorithm:

1. Quantum Speedup: Quantum algorithms can provide exponential or polynomial speedups over classical algorithms for specific problems.
2. Problem Domains:
   • Cryptography: Shor’s algorithm breaks RSA encryption by factoring integers efficiently​​.
   • Optimization and Search: Grover’s algorithm decreases the difficulty of finding solutions in large datasets​​.
   • Simulation: Algorithms for simulating quantum systems or solving physical equations, such as the Quantum Fourier Transform or the Harrow-Hassidim-Lloyd (HHL) algorithm, are fundamental in fields like quantum chemistry and materials science​.
3. Quantum Circuit Model: Algorithms are stated in terms of quantum circuits, sequences of quantum gates applied to qubits, and the fundamental units of quantum information​​.
4. Hybrid Techniques: Many algorithms combine quantum and classical computations, using quantum methods for specific sub-problems where they excel, such as optimization or eigenvalue problems

Applications:

1. Cryptography: Breaking classical cryptographic schemes and designing quantum-secure protocols.
2. Optimization and Search: Accelerating solutions to combinatorial optimization problems and search in large datasets.
3. Simulation: Modeling quantum systems in physics, chemistry, and materials science, which is computationally prohibitive classically.
4. Machine Learning and AI: Enhancing classical ML techniques using quantum methods like quantum neural networks and optimization.

Challenges:

1. Noisy Intermediate-Scale Quantum (NISQ) Era: Current quantum computers have limitations in qubit count and gate fidelity, which limit the execution of large-scale algorithms.
2. Data Encoding: Efficiently encoding and decoding classical data into quantum states remains a hurdle.

Types of Quantum Algorithms

Depending on their uses and underlying ideas, quantum algorithms may be generally divided into different forms.

Quantum Search Algorithms

For unsorted databases, Grover’s Algorithm provides a quadratic speedup over conventional methods. Through quantum state amplitude manipulation, this method increases the likelihood of discovering a desired solution.

Quantum Simulation Algorithms

• Quantum Phase Estimation: Essential for many quantum simulations, quantum phase estimation extracts eigenvalues of unitary operators.
• Harrow-Hassidim-Lloyd (HHL) Algorithm: Often employed in scientific and engineering simulations, the efficiently solves systems of linear equations with the Harrow-Hassidim-Lloyd (HHL) Algorithm.
• Quantum Approximate Simulation: Contains techniques for modeling physical systems including Quantum walks and product formulations under Quantum Approximal simulation.

Quantum Fourier Transform (QFT) Based Algorithms

• Among these are fundamental methods like the Quantum Fourier Transform, which are crucial for Shor’s and quantum phase estimation algorithms.
• Shor’s Algorithm solves discrete logarithms and integer factorization among other things.
  • Attacks elliptic curve, Diffie-Hellman, and RSA systems among others.
• Deutsch-Jozsa algorithm: Designed to ascertain if a given function is balanced—that is, outputs 0 for half of the inputs and 1 for the other half—or constant—that is, generates the same result for all inputs.

 Hybrid Quantum/Classical Algorithms:

These algorithms mix the advantages of quantum and conventional computing. Usually depending on conventional computers for other aspects of the process, they employ a quantum computer for particular computationally difficult chores.

• Quantum Approximate Optimization Algorithm (QAOA): Seeking approximate solutions to typically challenging-to-solve issues traditionally, the Quantum Approximate Optimization Algorithm (QAOA) adopts a hybrid technique to address combinatorial optimization problems.
• Variational quantum algorithms (VQAs): Often employed to discover the ground state of a Hamiltonian, therefore representing the energy of a quantum system, variational quantum algorithms (VQAs) use classical optimization techniques to direct quantum operations.
  • Variational Quantum Eigensolver (VQE): Approximates ground state energies in quantum chemistry and material science using Variational Quantum Eigensolver (VQE).
  • Variational Quantum Simulation (VQS): It effectively models quantum systems by use of hybrid quantum-classical methods.
    

Quantum Walk Algorithms

Using quantum walks as quantum analogues of classical random walks, one may investigate intricate networks and more effectively solve search issues.

• Boson sampling problem: Determining the probability distribution of bosons (particles following Bose-Einstein statistics) distributed via a linear optical network presents the boson sampling issue. Considered as a possible proof of quantum supremacy—that is, the capacity of quantum computers to surpass conventional computers on particular tasks—this is based on
• Element distinctness problem: Finding whether every element in a given list is unique is the element distinctiveness issue. For this problem, quantum walk-based techniques provide speedups over more traditional methods.

Quantum evolutionary algorithm (QEA)

links evolutionary algorithms with ideas from quantum computing. It uses quantum bits to depict in a quantum chromosome a superposition of many states. Greater population variety made possible by this might result in better solutions.

Quantum Particle Swarm Optimization Algorithm (QPSO)

Inspired by the behavior of particles in a swarm, this quantum algorithm mimicking quantum particles and their interactions investigates the search space.

Quantum Annealing Algorithm (QAA)

Quantum Annealing Algorithm (QAA) is a kind of quantum method applied in optimization tasks. It makes use of quantum annealing, a technique whereby the energy of a system is progressively altered to identify the ideal solution, therefore corresponding to the ground state of the system.

• The Quadratic Unconstrained Binary Optimization (QUBO) model allows both gate-based and annealing-based quantum computing techniques to address optimization problems.

Quantum Neural Network (QNN)

Inspired by the structure and operation of biological neural networks, this quantum method uses quantum features to execute computations and learn patterns from input.

Quantum Bayesian Network (QBN)

Quantum Bayesian Network (QBN) is a quantum computing application of Bayesian networks—probabilistic graphical models. It expresses and controls probabilistic connections using quantum states and actions.

Quantum Wavelet Transform (QWT)

Quantum Wavelet Transform (QWT) is a mathematical procedure applied in signal processing and data analysis whereby the wavelet transform is performed using quantum mechanics.

Quantum Clustering Algorithm (QC)

QC, or quantum clustering algorithm: Designed for grouping like data points, this quantum algorithm uses quantum characteristics to improve clustering methods.

How Does Quantum Algorithms Works in Quantum Computing

Quantum algorithms work on quantum computers by the principles of quantum mechanics like superposition, entanglement, and quantum interference. Here’s a stepwise explanation of how they work.

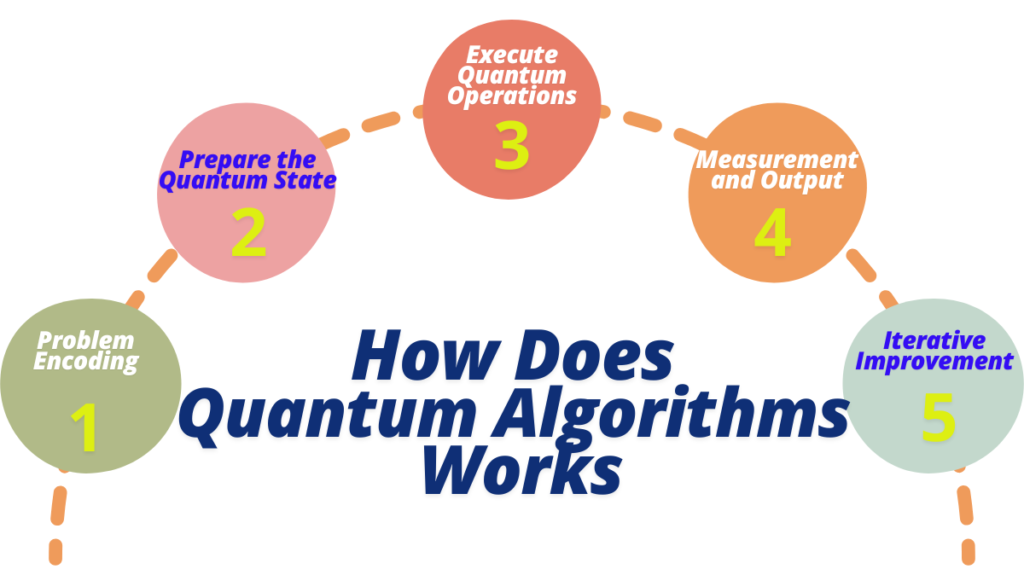
Step 1: Problem Encoding

1. Define the Problem:
   • The problem is first analyzed to determine whether it is suitable for a quantum solution. Examples include factorization, search, or simulation tasks.
   • Data is mapped onto the quantum domain, typically by encoding it into the quantum state of qubits.
2. Initialize Qubits:
   • Qubits are initialized into a specific quantum state, often |0⟩. The initial state must be carefully chosen to represent the problem.

Step 2: Prepare the Quantum State

1. Superposition:
   • Apply quantum gates (e.g., Hadamard gate) to create a superposition of all possible states. This allows the quantum computer to process multiple inputs simultaneously.
   • Example: In Grover’s algorithm, all potential solutions are placed in superposition.
2. Entanglement:
   • Create entanglement between qubits using gates like CNOT or controlled gates. Entanglement ensures that qubits are correlated, enabling complex operations.

Step 3: Execute Quantum Operations

1. Apply Quantum Gates:
   • Quantum gates (unitary operations) manipulate the state of qubits. These gates are the building blocks of quantum circuits and represent operations like rotations, flips, and entanglement.
   • Example: In Shor’s algorithm, modular exponentiation and Fourier transform are used to find periodicity.
2. Quantum Interference:
   • Use interference to amplify the probability of correct solutions while reducing the likelihood of incorrect ones.
   • Example: Grover’s algorithm amplifies the amplitude of the correct answer through repeated iterations.

Step 4: Measurement and Output

1. Collapse the Quantum State:
   • Measure the qubits, collapsing the superposition into a single classical state. The outcome represents the solution.
   • Probabilities are governed by the squared amplitudes of the states.
2. Classical Post-Processing:
   • Perform classical computations on the measurement outcomes if needed. For example, in Shor’s algorithm, post-processing is used to compute the prime factors from the periodicity.

Step 5: Iterative Improvement

1. Repeat and Refine:
   • Many quantum algorithms, like Grover’s, require iterative steps to converge on the correct solution.