The Bloch sphere is a geometric representation of the state space of a single qubit in quantum computing. It serves as a visualization tool for understanding quantum states and operations.
What is a Single-Qubit Bloch Sphere?
A qubit is the fundamental unit of quantum information, similar to a classical bit, but it exists in a superposition of states ∣0⟩ and ∣1⟩. The Bloch sphere visually represents this state in a three-dimensional space.
Representation of Qubit States in Bloch Sphere:
A qubit state ∣ψ⟩ can be expressed as:
∣ψ⟩=cos(θ/2)∣0⟩+eiϕsin(θ/2)∣1⟩
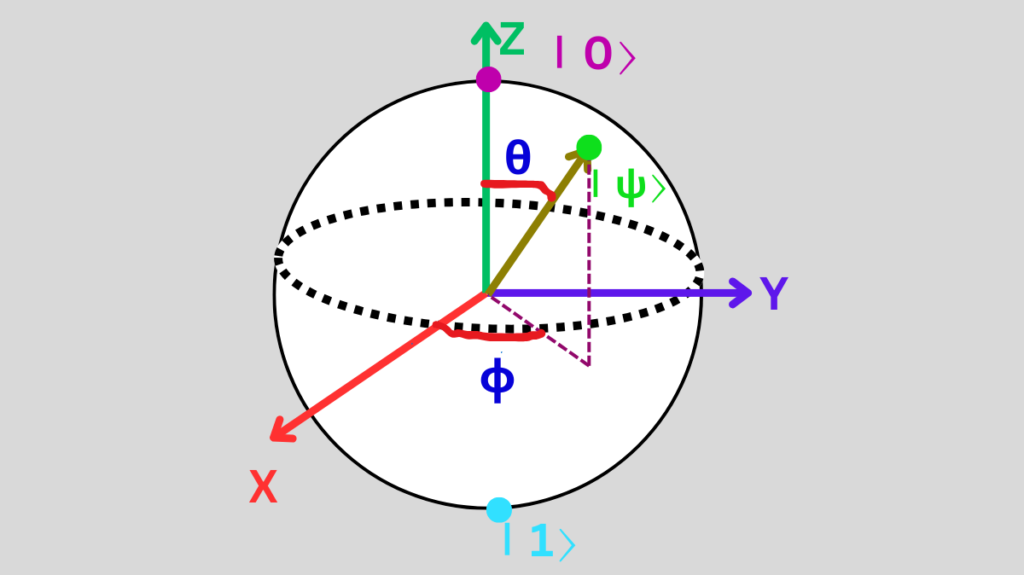
where θ and ϕ are spherical coordinates.
Here, θ (latitude) is the angle from the Z-axis, and ϕ (longitude) is the angle in the xy-plane from the x-axis.
Geometry of the Bloch Sphere
- Poles:
- The north pole represents ∣0⟩, and the south pole represents ∣1⟩.
- Equator:
- Superpositions like 1/2(∣0⟩+∣1⟩) lies on the equator at ϕ-0 and 1/2(∣0⟩−∣1⟩) lie along the equator ϕ-π.
- Axes:
- The z-axis represents the basis states ∣0⟩ and ∣1⟩.
- The x-axis and y-axis represent phase relationships between ∣0⟩ and ∣1⟩.
States on the Bloch Sphere
- Pure States:
- Represented by points on the surface of the sphere.
- Example:
- ∣+⟩=1/2(∣0⟩+∣1⟩) is on the equator along the x-axis.
- ∣−⟩=1/2(∣0⟩−∣1⟩) is on the equator in the negative x-direction.
- Mixed States:
- Represented by points inside the Bloch sphere.
- Pure states lie on the surface, while mixed states lie closer to the center.
- Global Phase:
- A global phase factor like eiγdoes not affect the physical properties of the state. Hence, the Bloch sphere only considers the relative phase.
Unitary Operations on the Bloch Sphere
- Quantum gates like Pauli X, Y, Z, and rotations can be visualized as rotations of the Bloch sphere:
- Pauli-X: Rotation by π about the x-axis.
- Pauli-Y: Rotation by π about the y-axis.
- Pauli-Z: Rotation by π about the z-axis.
- Rotations preserve the sphere’s radius, ensuring that states remain pure.
Advantages of Bloch Sphere in Quantum Computing
Visualization of Qubit States
- The Bloch sphere maps the complex quantum state of a single qubit to a point on or inside a sphere, making abstract mathematics easier to grasp.
- Qubit states ∣0⟩ and ∣1⟩ are clearly represented as the north pole and south pole of the sphere.
- Superpositions and phase differences between the states are represented as points on the equator or at any position on the surface.
Representation of Pure and Mixed States
- Pure states lie on the surface of the sphere.
- Mixed states are represented by points inside the sphere, with the distance from the center indicating the degree of “purity” of the state.
- This distinction between pure and mixed states is critical for analyzing noise and decoherence in quantum systems.
Geometric Interpretation of Quantum Gates
- Quantum gates, which perform operations on qubits, can be visualized as rotations of the Bloch sphere about specific axes:
- Pauli-X: Rotation around the x-axis (bit flip).
- Pauli-Y: Rotation around the y-axis.
- Pauli-Z: Rotation around the z-axis (phase flip).
- General unitary transformations correspond to arbitrary rotations of the sphere.
This geometric view simplifies the understanding of quantum operations and their effects on qubit states.
Visualization of Relative Phases
- The longitude angle (ϕ) on the Bloch sphere represents the phase difference between ∣0⟩ and ∣1⟩.
- This makes the Bloch sphere an effective tool for visualizing how quantum gates change the relative phase of quantum states.
Example:
- A rotation around the z-axis only changes the phase of the qubit without altering its amplitude.
Understanding Quantum Measurement
- Quantum measurements in the computational basis (∣0⟩) can be visualized as projecting the qubit state onto the z-axis.
- The probability of measuring ∣0⟩ or ∣1⟩ corresponds to the square of the projection lengths onto the north or south poles.
Simplified State Manipulation
- Using the Bloch sphere, quantum states can be manipulated geometrically using rotations, which are easier to comprehend than abstract matrix operations.
- This helps visualize algorithms like quantum teleportation and quantum gates.
Compact Representation of Single-Qubit States
- The Bloch sphere captures all possible pure states of a single qubit in a compact, finite-dimensional form.
- It avoids the complexity of infinite-dimensional Hilbert space representations.
Educational and Analytical Tool
- The Bloch sphere serves as an essential tool for teaching and analyzing quantum mechanics and quantum computing.
- It helps students and researchers intuitively understand key concepts like:
- Superposition
- Phase
- Entanglement (when multiple Bloch spheres are considered)
- Quantum state evolution
Facilitates Understanding of Noise and Decoherence
- Noise in a quantum system can be visualized as the qubit state moving from the surface of the Bloch sphere toward the center (mixed state).
- This aids in designing error-correction protocols to maintain the purity of quantum states.
Universality for Single Qubits
- The Bloch sphere provides a universal framework for representing any single-qubit quantum operation and state. This universality simplifies analysis and design in quantum computing.

