Mathematical Representation of Qubits in Quantum Computing

A quantum bit, also known as a qubit, serves as the fundamental unit of information in quantum computing, similar to a bit in classical computing. Unlike a conventional bit, a qubit can exist simultaneously in two states in superposition. This special quality results from the ideas of quantum physics, which control atom and subatomic particle activity.

Mathematical Representation of Qubits

Dirac notation:

A qubit possesses two quantum states similar to classical binary states. The qubit can exist in either state or in a superposition of both states simultaneously.These quantum states are represented using Dirac notation. The state label is enclosed between the symbols | and ⟩. States are represented as |0⟩ and |1⟩, which possess analog values. Both states contribute to yield any value between 0 and 1, provided that the sum of the probabilities of each state equals 1. Any quantum bit wave function can be represented as a linear combination of two states, each associated with a complex coefficient, specifically: |w⟩ = x |0⟩ + y |1⟩, where x and y denote the coefficients of the respective states. The probability of a state is directly proportional to the square of the magnitude of its coefficient. The expression |x|² represents the probability of identifying the qubit state 0, while |y|² denotes the probability of identifying the qubit state 1. The sum of these probabilities must equal 1, or 100% mathematically, expressed as |x|² + |y|² = 1.

Vector Notation:

The state of a qubit is represented as a vector, specifically as a single column matrix illustrated in the figure below. The term “quantum state vector” is used interchangeably and must satisfy the normalization condition, specifically |a|² + |b|² = 1. Here, the squared absolute values of a and b denote the probabilities of the qubit collapsing to either state upon measurement, typically favoring the state with the higher probability. In summary, |a|² represents the probability of collapsing to 0, while |b|² denotes the probability of collapsing to 1; thus, their sum must equal 1 to ensure absolute certainty.

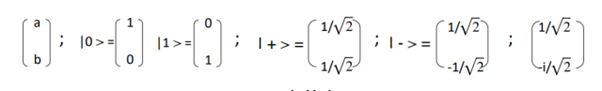
The matrices depicted in the figure represent all permissible quantum state vectors. The components of the state vectors may be represented as complex numbers. A complex number can be represented as a + ib, where a and b denote the abscissa and ordinate in a two-dimensional Cartesian plane, or in exponential form Aeiω, with A representing the radial coordinate and ω indicating the angle in a polar reference frame. It is important to recognize that a, b, A, and ω (expressed in radians) are real numbers, while i represents the imaginary unit.

Bloch Sphere:

The state of a single qubit can be visually represented as a point on the surface of a sphere called the Bloch sphere.

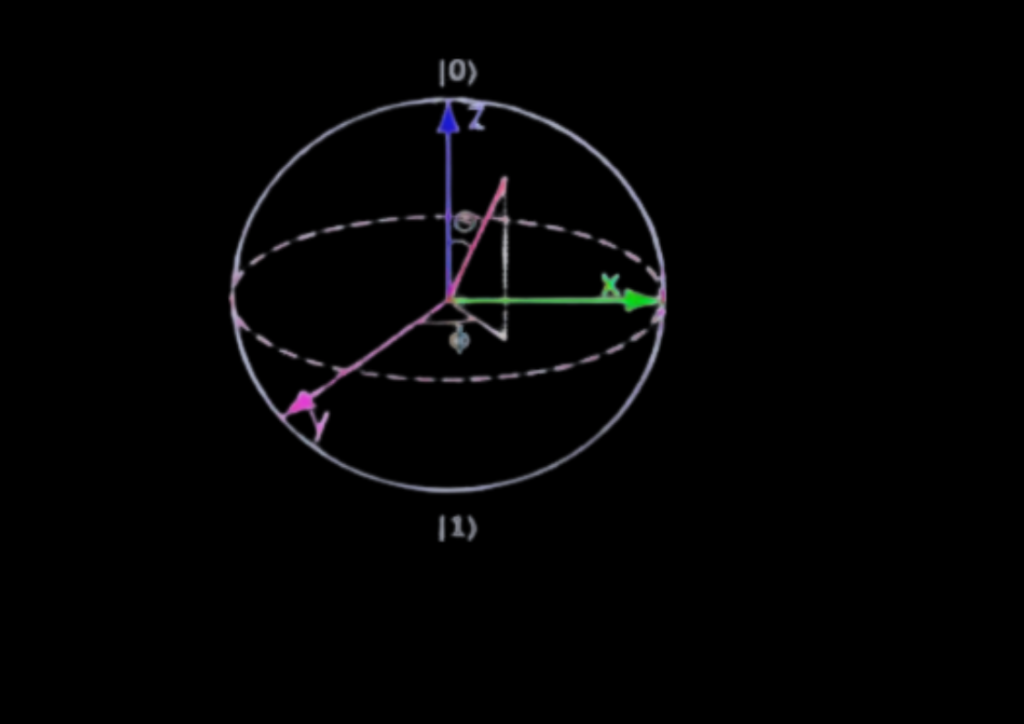
• The north and south poles of the sphere represent the basis states |0⟩ and |1⟩, respectively.
• Points on the surface of the sphere represent different superpositions of the basis states.
• The Bloch sphere representation is useful for visualizing single-qubit operations, but it doesn’t generalize well to multiple qubits.

Multiple Qubit Systems

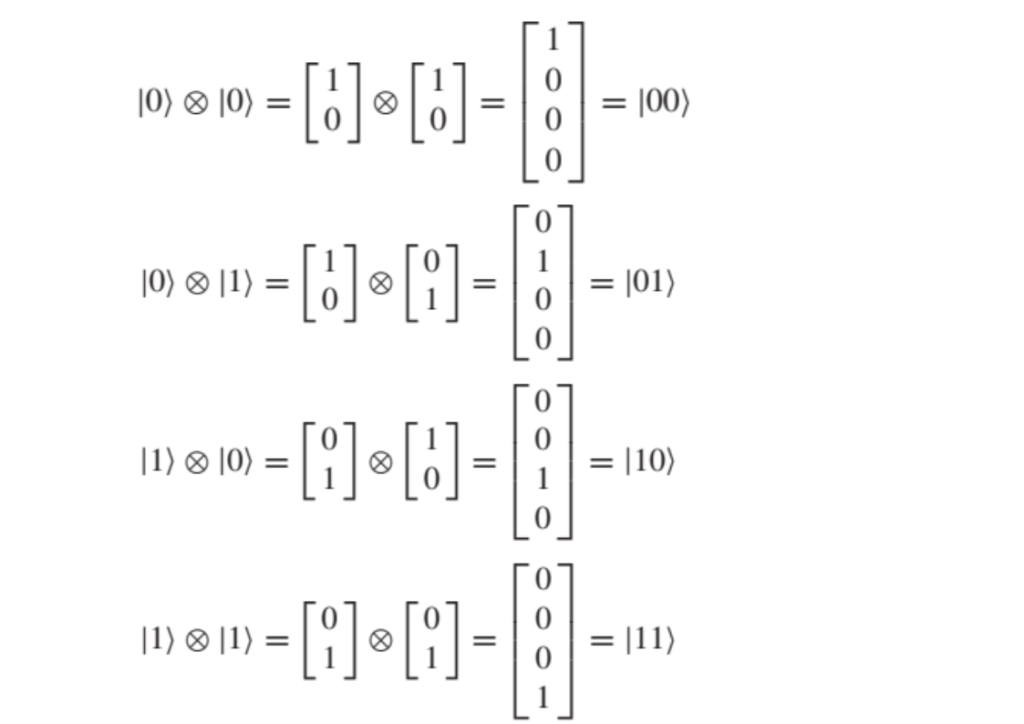
Systems with several qubits Specifically, the tensor product is applied in mathematics. Direct product and Kronecker product are alternative names for the tensor product. One way to describe tensor product is as: If the matrix M is p × q and the matrix N is x × y, then the tensor product (MN) is a (px) × (qy) block matrix that represents the state of the multiple-qubit system. Matrix multiplication—the mathematical analogue of a quantum gate applied to a quantum system—is distinct from this. How about we define the matrices as

Tensor products of matrices of higher orders can also be calculated in the same way. In dirac notation, the tensor product of the following quantum states is the same as

Key Concepts

• Superposition: Unlike conventional bits, qubits can exist in a superposition of both states concurrently.
  
• Probability Amplitudes: The complex numbers known as probability amplitudes—whose squared magnitudes indicate the qubit’s likelihood of measurement in the appropriate basis states—are the coefficients in the linear combination expressing a qubit state.
  
• Entanglement: Multiple qubits entangled have their states linked in a way that cannot be explained by separately examining each qubit. Though they highlight entanglement as a fundamental idea in quantum computing, the sources offer no mathematical explanation of it.
• Measurement: Measuring a qubit collapses its superposition into one of the basis states; the probability amplitudes then decide the outcome probabilistically.
  
• Unitary: A unitary matrix preserves the normalizing condition of the probability amplitudes, therefore characterizing the evolution of a qubit state.

These mathematical Representation offer the structure for comprehending qubit information storage and manipulation capability to execute calculations in quantum algorithms.